Perigordtruffle - Hunting For Rabbit Holes

The Lambda Calculus and Typed De Bruijn Indices

I thought I'd write up another little post about something in CS that I think is cool. This one is about variable binding and types, with some Haskell code (with GADTs and pseudo-dependent types) later on.

In other words, this is going to be a bunch of math and logic and then some Haskell nonsense. Be warned.

So, to start off: the lambda calculus. Extremely simple language that just has functions (that you write with a λ), and function application. We can write the identity function as (λ x. x), which we can read as "a function that takes x as input and returns that same x." A function that takes two arguments and returns the first can be written as (λx. λy. x), and a similar function that returns the second argument would be written as (λx. λy. y). Function application works straightforwardly, so (λ x. x) 42 evaluates to 42, and (λx. λy. y) 69 420 evaluates to 420.

To write out our functions like this we use variables, typically one letter. This is convenient---there's a reason basically every popular programming language uses variable names---but it has some downsides. To get to that, let's talk about alpha equivalence.

If we have two functions, (λ x. x) and (λ y. y), what can we say about them? Well, they both just return whatever their argument is. They're actually both the same function; they're both the identity function.

Of course, in general, determining if two arbitrary functions are equal is a little complicated. One definition of equality for functions is called function extensionality, which says that two functions are equal if they always produce the same output from every input (if for all x, f(x) = g(x), then f = g), and that can be tricky to deal with. But our two functions, (λ x. x) and (λ y. y), are literally written the same, except for a switched-out variable name!

That notion of two functions being written exactly the same except for different chosen variable names is called alpha equivalence. (λ x. x) and (λ y. y) are alpha equivalent. This captures the intuitive idea that changing variable names won't change what the program does, as long as they don't clash or overlap.

The Dutch mathematician Nicolaas Govert de Bruijn came up with an alternate notation for these functions that made this explicit. Instead of using names, you use numbers. So (λ x. x) becomes (λ 0), for example, and (λx. λy. x) becomes (λ λ 1). You can read the number as something like "starting from here and working backwards, this is how many lambdas to jump over," (beginning at 0 of course). So the 1 in (λ λ 1) is referring to the binding from the first lambda, whereas in (λ λ 0) the 0 is referring to the binding from the second lambda.

This illustration from Wikipedia represents how to write the lambda calculus program λz. (λy. y (λx. x)) (λx. z x) using De Bruijn indices:

One immediately neat thing about this is that it makes alpha equivalence trivial. Both (λ x. x) and (λ y. y) are now just written (λ 0).

Another benefit of this approach is that it is particularly convenient when doing formal reasoning about programming languages. To get into that, first I'll explain types and the lambda calculus.

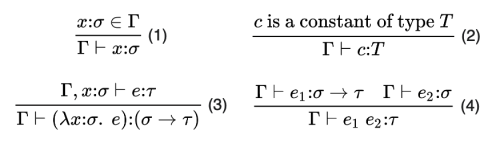
This is a common presentation of the typing rules for a language called the simply-typed lambda calculus. You can read the lines as "if what is above the line is true, then what is below the line is true," and the things that look like Γ ⊢ x : t as "assuming type environment Γ we can prove x has type t." Going through each rule:

If from assumed type environment Γ we know x has type σ, then we can prove x has type σ.

If some constant c has type T, then we can prove c has type T.

If we assume x has type σ, and from that conclude e has type τ, then we can prove (λx:σ. e) has type σ → τ (where the x:σ bit is a type annotation).

If we know e1 is a function of type σ → τ, and we know e2 is of type σ, then if we apply (e1 e2) then the result we get will have type τ.

Basically, Γ contains a list of (variable:type) pairs, because it records the assumptions of what the type of each variable is assumed to be.

So, let's throw out all those variables! If we use De Bruijn indices, then Γ is just a list of types. This makes it very convenient to work with in the setting of something like a proof assistant, or a programming language with dependent types.

Now I'll show how we can use all of this to write a so-called "type-safe interpreter" in Haskell. This is actually a somewhat common example program to write in a dependently typed language, because it's relatively simple (ha!) and it shows off some of the neat things you can do with types.

This post is already getting long so I'll jump right to the code. This is a data type for encoding the STLC:

This is a GADT, or generalised algebraic data type. It is parameterised by two types: the type environment, and the result type. So 'Expr as a' can be read as "a program that assumes type environment as and will produce a value of type a." If you look closely, you'll see that the constructors of this data type declaration line up with the numbered rules above.

This is a definition of a very simple AST, or abstract syntax tree, for a language. Can we write an interpreter for our language that uses this data type? Yes!

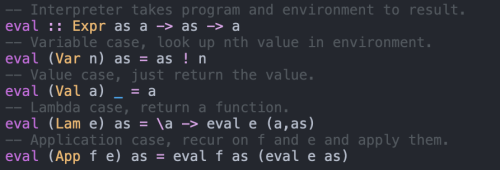
Before we can actually run it we need to get the rest of the definitions out of the way. First, natural numbers, typical peano numbers:

Then the Index typeclass, for indexing into type environments:

With all that done, we can interpret some programs!

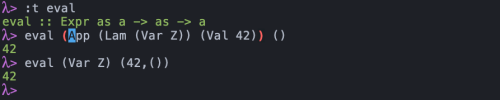
That's it! We call this a "type-safe interpreter" because we have a guarantee that the program is well typed, and we have a guarantee that the interpreter is respecting those types. Isn't that cool?

Reblog to give a trans girl a random robotic body part

Reblog if your inbox is ALWAYS open for random asks, even if you haven’t reblogged any meme

Anyone else learn languages designed to be proof assistants? Or atleast designed with theorem proving as a usecase. Whilst barely knowing any pure Math?

When I first started learning Idris2, I had no idea how to even structure a proof. Needless to say I was quite lost, even if I was experienced in Haskell at that point.

Even now when I'm learning Lean, when I started which was about 5 days ago, I only knew how to prove with truth tables. It wasn't until yesterday when I found about the logics other than Classical.

So basically all I know about pure math is just me brute-forcing my way into learning languages like Idris as well as the occasional Haskell article or codewars kata ethat deep dives into a concept.

It wasn't until recently when I decided to finally sit down and learn Pure Math starting from basic Discrete Math. It's fun because I keep recognizing the concepts that's become commonplace in the languages I use. I learned about Connection intros and eliminations before knowing the difference between classical and intuitionistic logic.

What I'm saying is I love Curry-Howard correspondence

Welp

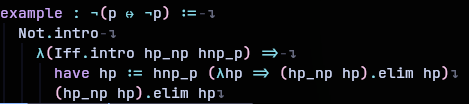
as expected I had greatly overestimated the problem.

Atleast I learned the basics of Constructive and Modal logic.