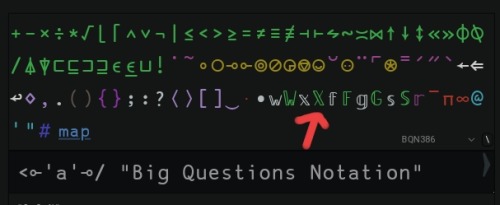
19 | Trans + Aroace | Programming and Drawing and Stuffs
154 posts
Day 5 Of Learning Lean
Day 5 of learning Lean
why is proving ¬(p ↔ ¬p) so hard
Of course with Truth tables and classical logic, this is near trivial to solve. In fact here's the proof
example : ¬(p ↔ ¬p) := Not.intro λ(Iff.intro pnp npp) => have hnp : ¬p := (imp_iff_not_or.mp pnp).elim id id have hp : p := npp hnp hnp.elim hp
Could be a lot shorter, especially at proving the (¬p ∨ ¬p) part. But you get the gist.
Unfortunately this line exists

imp_iff_not_or is apparently only in classical logic, because it relies on the law of excluded middle which is (p ∨ ¬p) which intuitionistic logic does not have as ¬p is defined as (p -> False).
right now I'm looking into modal logic for solutions and it seems promising, having translations from Intuitional to KT4 modal logic, though I still don't know how I could translate it to a lean solution. It's also very likely there is a simpler solution that I am not seeing.
Either way, it's pretty fun despite my frustrations.
So far still stuck at page 3 of theorem proving in lean 4, though I only have 1 problem to solve.
More Posts from Perigordtruffle
Curry-howard correspondence is a neat little thing.
Tuples are equivalent to And
Sum Types are equivalent to Or
atleast Exclusive Or I think, since you can't have an `Either p q` be both `Left p` and `Right q` at once. They'd need to be more like `Either a (Either b (a,b))`
Keep in mind that `a,b` can be any type, not just booleans. It's not so much a comparison as much as it just says if the type exists.
(Exists in the way there's a representation of it in code.)
For the longest time I just thought it was just some cool equivalence. I've never really utilized this concept until I've used Lean which actually utilizes this concept. Proving two statements are equivalent means creating an isomorphism between both of the types.
For example
Proving
(P ∨ Q) ∨ R = P ∨ (Q ∨ R)
Is similar to proving the Isomorphism
Either (Either P Q) R
<=> Either P (Either Q R)
(a <=> b is equal to a -> b and b <- a) btw
And
Proving
(P ∧ Q) ∧ R = P ∧ (Q ∧ R)
Is similar to making the Isomorphism
((P,Q),R) <=> (P,(Q,R))
(Though of course And is easier due to the inclusivity thing I mentioned earlier)
is it normal that I'm 18 and I still have absolutely no concept of romantic/sexual attraction or relationships
I ... think I'm bisexual? maybe? but it would be really nice if I could find at least one person that I'm actually attracted to so I can confirm that
whenever I try to think about my sexuality I feel like I'm blindfolded and throwing darts at a board labeled with genders
In a random town, a serial killer names themselves "Corpse Man". They were born with the ability to see people as corpses, not as the way they would die but simply seeing as though they were a corpse with the way they die having no correlation to anything. This has given them a particularly warped view of the world, seeing living as an intermediary step between being objects.
In the same town a new hero arises, publicly named "Corpse Man". They are of a man long dead, even though they are inanimate they appear to do heroic acts. The acts are regular enough to have the town formally recognize them as an upholder of the law. They even have a government-paid embalming team to ensure they are able to do heroic acts without scaring the public. Going against the killer's ideals, they swiftly made the corpse a mortal enemy of his. Somehow they find themselves regularly defeated by this inanimate corpse.
Eventually after enough loses, an epiphany arrives to the killer and...
Message #off-topic
Does anyone have any objections??